Мозаика Пенроуза, или как среднеазиатские зодчие на пять веков предвосхитили открытие европейских учёных Разное

В февральском номере журнала «Сайнс» («Science») за 2007 год появилась статья американских ученых Питера Лу и Паула Стейнхардта о средневековой исламской архитектуре, сразу же ставшая научной сенсацией. По мнению авторов статьи, мозаичные узоры, украшающие стены средневековых мавзолеев, мечетей и дворцов, выполнены с использованием математических законов, открытых европейскими учеными лишь в 70-х годах ХХ столетия. Отсюда, со всей очевидностью следует, что средневековые зодчие на несколько столетий опередили своих европейских коллег.

Это открытие, как и многое в современной науке, произошло совершенно случайно. В 2005 году аспирант Гарвардского университета Питер Лу приехал в качестве туриста в Узбекистан. Любуясь настенным декором мавзолея Абдуллахана в Бухаре, он усмотрел в нем аналог сложных геометрических построений, изучавшихся им когда-то в университете. Причудливые формы узоров на многочисленных самаркандских орнаментах лишь подтверждали правильность его догадки. По возвращении домой он рассказал о своем открытии руководителю своей студенческой дипломной работы, профессору Принстонского университета, Паулу Стейнхардту.

Тщательное исследование структуры настенных росписей и орнамента средневековых мусульманских архитектурных памятников в Узбекистане, Афганистане, Иране, Ираке, Турции и Индии подтвердили правильность догадки Питера Лу и стали предметом упомянутой выше сенсационной статьи.

Для того чтобы понять смысл открытия Питера Лу и Паула Стейнхадта следует познакомиться с такими понятиями как задача о паркетах, квазикристаллическая структура, золотое число и т.д. Поэтому начнем изложение по порядку.

Задача о паркетах и структуры Пенроуза

В математике задача сплошного заполнения плоскости многоугольниками без пробелов и перекрытий называется паркетами. Еще древним грекам было известно, что эта задача легко решается при покрытии плоскости правильными треугольниками, квадратами и шестиугольниками.

В тоже время, правильные пятиугольники не могут служить элементарными элементами паркета, поскольку их нельзя на плоскости подогнать друг к другу плотно без зазоров. Тоже самое можно сказать о семи-, восьми-, девяти-, десяти- и т.д. угольниках. Постепенно были придуманы способы заполнения плоскости правильными многоугольниками разных видов и размеров. Например, вот так можно заполнить плоскость, комбинируя четырех- и восьмиугольники разных размеров:

Значительно более сложным развитием этой задачи было условие, чтобы структура паркета, составленного из нескольких видов многоугольников и полностью покрывающего плоскость, была бы не совсем «правильной» или «почти» периодической. Долгое время считалось, что эта задача не имеет решения. Однако в 60-х годах прошлого столетия она все же была решена, но для этого понадобился набор из тысяч многоугольников различных видов. Шаг за шагом число видов удавалось уменьшить, и, наконец, в середине 70-х годов, профессор Оксфордского университета Роджер Пенроуз решил задачу, используя всего два вида ромбов. Ниже показан вариант квазипериодического (т.е. почти периодического) заполнения плоскости ромбами с острыми углами в 72 и 36°. Их еще называют «толстыми» и «худыми» ромбами.

Для получения непериодической картины при укладывании ромбов следует придерживаться некоторых нетривиальных правил их сочетания. Оказалось, что эта простая с виду структура обладает очень интересными свойствами. Например, если взять отношение числа тонких ромбов к числу толстых, то оно оказывается всегда равно так называемому «золотому сечению» 1,618… Поскольку это число «не точное», а как говорят математики иррациональное, то и структура получается не периодической, а почти периодической. Более того, это число определяет соотношение между отрезками внутри десятиугольников, образующих пятиконечную звезду – пентаграмму, которая считается геометрической фигурой с идеальными пропорциями. Обратите внимание, что выделенные десятиугольники имеют одинаковую ориентацию, что согласовывает и определяет расположение ромбов, из которых составлена мозаика Пенроуза. Поразительно, что это чисто геометрическое построение оказалось самой подходящей математической моделью для описания, открытых в 1984 году квазикристаллов.

Что такое квазикристаллы

Мы включили этот раздел в нашу статью для того, чтобы рассказать еще одну интересную историю о том, как математическое построение, являющееся плодом чистой фантазии ученых, неожиданно нашло важное практическое применение.

Все вещества в природе можно разделить на два типа: аморфные, в которых полностью отсутствует закономерность во взаимном расположении атомов, и кристаллические, характеризующиеся их строго упорядоченным расположением. Из законов кристаллографии следует, что для кристаллов возможны оси симметрии лишь первого, второго, третьего, четвертого и шестого порядков, т.е. по аналогии с паркетами кристаллы с симметрией пятого порядка в природе существовать не могут. Это обстоятельство было строго доказано на основе математической теории групп в многомерных пространствах. Но природа, как всегда оказалась намного изобретательней и в 1984 году была опубликована работа группы Шехтмана, в которой сообщалось об открытии сплава алюминия с марганцем, обладающего вращательной симметрией пятого порядка. Впоследствии было синтезировано множество аналогичных сплавов с неизвестными доселе свойствами. Эти сплавы были названы квазикристаллами, и сейчас они рассматриваются как промежуточные между аморфными и кристаллическими формами вещества.

Именно благодаря этому открытию геометрическое построение Пенроуза, оказавшееся наиболее подходящим инструментом для моделирования структуры квазикристалов, приобрело большую известность и получило дальнейшее развитие. И именно поэтому оно включено в университетские курсы. В настоящее время уже получено трехмерное обобщение мозаики Пенроуза, составленной из худого и толстого ромбоэдров — шестигранных фигур, каждая грань которых — ромб.

Какая геометрия лежит в основе средневековой мозаики

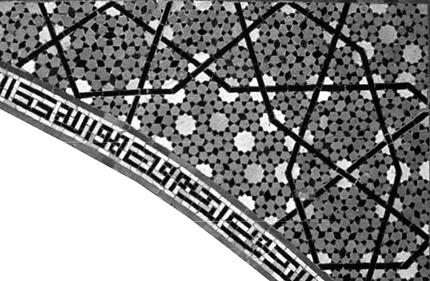
Проанализировав около 3700 мозаичных плиток, Лу и Стейнхардт пришли к заключению, что на рубеже XIII века повсеместно в мусульманских странах распространилась технология декорации мавзолеев, мечетей и других строений периодической мозаикой, составленной из набора пяти многоугольников, а именно, десятиугольника, шестиугольника, галстука-бабочки (терминология авторов статьи), пятиугольника и ромба. По существу, это было решение описанной выше задачи о паркетах с помощью набора из пяти «мусульманских» многоугольников. Узоры, составленные из таких многоугольников, называются «гирих» (от персидского – узел).

Обратите внимание, что грани всех многоугольников имеют одинаковые размеры, что позволяет состыковывать их с любой стороны. Кроме того, на каждой плитке-многоугольнике имеются декорирующие линии, но и они прочерчены по строгим геометрическим правилам: любые две линии узора сходятся в середине каждой стороны под углами в 72 или 108°, т.е. кратными 36°. Это обеспечивает сохранение непрерывности узора при переходе от одной плитки к другой.

Для построения такой мозаики было достаточно иметь в своем распоряжении циркуль и линейку. Кстати, до открытия американских ученых так и считалось, что средневековые мастера при создании декора зданий пользовались лишь простейшими инструментами как линейка и циркуль. Теперь стало очевидным, что это не совсем так.

На XV век приходится самый созидательный период расцвета науки и культуры в странах, управлявшихся Тимуридами. Именно в это время произошел качественный скачок и в искусстве орнамента. Подтверждением этого является, тот факт, что многочисленные исследованные памятники как мавзолей Дарб-е-Имама в Иране, усыпальница Хаджа Абдуллаха Ансари в Герате и другие относятся к эпохе Тимуридов.

Комбинация ставшей к этому времени традиционной мозаики гирих, и геометрических фигур «стрела» и «бумажный змей» (опять по терминологии Лу и Стеинхардта) позволили создать

непериодические узоры, напоминающие мозаику Пенроуза. Отсюда следует, что к этому времени они, возможно, использовали более сложные инструменты, но совершенно очевидно, что в XV веке в технике декора произошел концептуальный скачок!

Уже в последующих, после опубликования статьи, интервью Лу и Стейнхардт отмечали, что они не могут сказать, насколько средневековые зодчие сами понимали детали своего открытия, но то, что они видят это аналог структур Пенроуза. И они совершенно уверены в том, что то, что они открыли, не может быть лишь каким-то случайным совпадением.

Лирическое отступление

Дело сделано. Мне удалось разобраться в премудростях геометрических узоров, придающих неповторимую красоту творениям наших предков, и я надеюсь, в какой-то степени удовлетворить любопытство наших соотечественников. Остается, конечно, какая-то неудовлетворенность, ведь я тоже сотни раз любовался красотой и изяществом самаркандских орнаментов. Почему же мне никогда не приходила в голову эта мысль. В оправдание себе могу лишь сказать, что, когда квазипериодическая структура Пенроуза вошла в университетские курсы, я уже работал над кандидатской диссертацией по своей узкой специальности. А Питеру Лу всего 28 лет, и он уже проходил структуры Пенроуза в университете. Конечно, знать и распознать в совершенно неожиданном месте проявление какой-нибудь закономерности совершенно разные вещи, но, чтобы это сделать, надо как минимум знать, что такой закон существует.

Но лирическое отступление не об этом. Для того чтобы разобраться в сути статьи в журнале «Сайнс» мне понадобилось два дня, вернее две бессонные ночи, но причины, по которым я не сделал этого раньше, имеют, как мне кажется, глубокий философский смысл. Когда я прочел в Интернете информацию о статье Лу и Стейнхардта, то я сразу же позвонил моему коллеге, специалисту в области геометрии. Он с полуслова понял, о чем идет речь, но огорчил меня, сообщив, что я застал его перед отъездом в аэропорт. Узнав, что он возвращается из зарубежной командировки только через три месяца, я попросил его хотя бы рекомендовать мне какую-либо книжку, в которой я мог бы прочитать о структурах Пенроуза. Он назвал мне книжку и при этом добавил, что это очень сложная математика и вряд ли можно будет быстро все понять и тем более объяснить это популярно обычным людям. Когда я пролистал рекомендованную мне книгу, напичканную такими понятиями как, многомерные инвариантные пространства, фактор-пространство сопряженного иррационального пространства, то мой энтузиазм быстро угас.

После сообщения информационного агентства «Жахон» интерес нашей научной, да и не только научной общественности к этому вопросу стал лавинообразно нарастать. Среди ученых мужей Академии наук и Национального университета, конечно, нашлись специалисты, которые разбираются в сложных вопросах алгебр Ли, теории групп, многомерных симметрий и т.д. Но все они, были едины во мнении, что объяснить эти вещи популярно невозможно. На днях меня внезапно осенила тривиальная мысль: Постой. А как же додумались до этого средневековые зодчие, ведь они не располагали мощнейшим аппаратом современной математики? На этот раз я решил попытаться понять это не через сложный математический аппарат квазипериодической структуры Пенроуза, который оказался для меня тёмным лесом, а пойти путем средневековых зодчих. Для начала я скачал из Интернета оригинальную статью Лу и Стейнхардта. Их метод меня поразил. Для объяснения сути своего открытия они тоже пошли именно этим путем, т.е. используя понятийный аппарат средневековых зодчих, и оперируя такими простыми вещами как мозаика «гирих», плитки «стрела», «бумажный змей» и т.д.

Философский смысл всего этого состоит в том, что для того чтобы понять законы природы (а может быть и общества) не обязательно всем идти одним и тем же путем. Человеческое мышление тоже многомерно. Есть восточный подход, и есть подход западный. И каждый из них имеет право на существование, и в отдельном конкретном случае может неожиданно оказаться более эффективным, чем противоположный. Так получилось и в данном случае: то, что удалось открыть западной науке на основе огромного обобщения тернистого опыта, восточная наука сделала на основе интуиции и чувства прекрасного. И результаты налицо: в практическом воплощении законов геометрии в практику, восточные мыслители опередили западных на пять столетий!

Шухрат Эгамбердиев.
Астрономический институт АН РУз.

С полным текстом статьи с цветными иллюстрациями можно ознакомиться в ближайшем (статья написана году в 2008. ЕС) номере журнала «Фан ва турмуш» — «Наука и жизнь Узбекистана».